「旧暦」=古い暦ですから、それに対して、現在の暦は「新暦」ということになりますが、では、この二つの違いは?というと、暦を定める上で、何を拠り所にしているかということでしょうか。
古く日本で使われていたのは「月」を基準にした「太陰暦」と呼ばれる暦でした。
これは新月(朔)から、満月(望)、そして、再び新月(朔)となる期間を1ヶ月とするものです。
高度な観測機器のない時代にあっても、夜空に浮かぶ月の変化なら、人の目で十分観測可能ですから、自然な流れだったといえます。
月の満ち欠けの周期を表す朔望月は29.530589日〈端数の部分は約12時間44分2.82秒〉。
そこで1ヶ月の日数を29日か30日とし、29日までの月を「小の月」、30日ある月を「大の月」などといいました。(現在は31日ある月を「大の月」、それ以外を「小の月」と呼んでいますね)
ただ、現在の新暦と違って、月ごとに29日なり30日なりの日数が定まっているわけではなく、年によって、1月でも29日までしかないことも、2月なのに30日まであることもありました。
ですから、公卿日記などに2月30日という日付が出てきたとしても、別に誤植でも何でもありません。
陰暦の便利な点は、朔が1日、満月が15日と、月齢がそのまま日にちになっていますから、日付がわかりさえすれば、その日の夜空の様子はおよそ推測することができます。
3日の宵とくれば西の空に三日月が、15日の深更なら南の空高くに満月が…。
間違っても、1日に満月とか、15日に三日月が見られるはずはないのです。
こうした月の満ち欠けのサイクルさえ知っていれば、後は夜空を見上げるだけで一目瞭然のことですから、この「太陰暦」は人の暮しに馴染みやすく、今も農作業などには陰暦を用いられる場合が多いようです。
しかし、一見便利なような太陰暦も、使い続けて行くと、どうしてもある問題点にぶつかることになります。
1ヶ月の日数が平均29.5日とすると、12ヶ月で約354日になります。一方、太陽暦では1年は約365日ですから、両者の間には11日程度の日数の差が生じることになります。
実際の季節は、今も昔も太陽暦通りに移り変わって行きますから、年を重ねるごとにその差はどんどん広がって…、例えば、1月の蝉時雨とか、8月の雪景色とか…、何とも奇妙なことになってしまいます。
さすがに、これはまずいということで、調整のために、閏月(うるうづき)なるものが考案されました。
計算上、年間にして10日程少ないわけですから、3年に1度の割合で、1ヶ月増やせばこのズレを解消できることになります。
この閏月も、3年毎というようにキッカリ決まった年に設けられるわけではなく、置閏法(ちじゅんほう)と呼ばれるある法則にのっとって、随時定められました。
では、その法則は…というと、「二十四節気」と呼ばれるものが関係して来ます。
「二十四節気?」と思われるかもしれませんが、「立春」「春分」などを例に挙げると、ご納得いただけるのではないでしょうか。
簡単にいうと、1年を24等分して、その区切りの日に名前をつけたものです。
| ||||||||||||||||||||||||||||||||||||||||||||
| ※( )内は新暦での相当日になりますが、年によって 1日程度前後します。 |
おそらくは、まず夏至・冬至・春分・秋分の二至二分が決められ、次いで立春・立夏・立秋・立冬を加えた八節の基本形ができ、やがてこれが細分化されて二十四節気となったと考えられます。
左側の「節」は季節の変わり目を決めるもの、右側の「中」が月名を決定するものとされています。
ここで重要なのは、あくまでも月の満ち欠けが先で、その朔望月の1周期中に含まれる「中」の月名を付すことです。
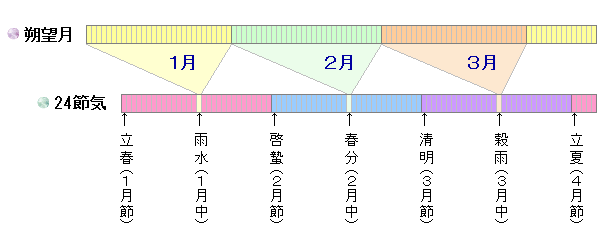
ところで、太陽暦による1年は、少し細かく言うと約365.24219日。「中」は年間12回ですから、単純に12等分すると、約30.436849日になります。
一方、月の朔望周期は29.530589日ですから、その差は約0.90626日と、わずか1日弱ながら、朔望周期の方が短いことになります。
ということは、この差が積もりに積もると、33〜34朔望周期に一度の割合で、「中」が一度も現れないという現象が起こることになります。
| 「中」の 間隔 月の朔望周期 |
365.24219日 ÷ 12月 ≒ 30.436849日 29.530589日 |
||
| 差 引 | 0.906260日 | ||
| 「中」が現れない割合 = 30.436849日 ÷ 0.906260日 ≒ 33.585118(朔望周期) | |||
この場合「中」がないわけですから、その月に名前をつけることができません。だからといって、次の月名をつけてしまえば、翌月の月名がなくなってしまいますし、名無しのまま放置するわけにもいかず…。
そこで、直前の月の名前に「閏」をつけて、例えば直前が7月であれば、閏7月とすることにしたわけです。
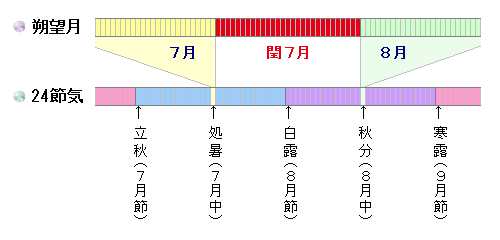
このような太陰暦と太陽暦のミックスされた太陰太陽暦が、今呼ぶ所の旧暦に当たり、明治維新で太陽暦が採用されるまで、日本ではこれを正規の暦としていました。
しかし、こうして辻褄合わせをしても、今度は閏月のある年は、日数が380日余りになるという、新たな矛盾を生むことになり、スッキリ解消とは行きませんでした。
|
|
